シミュレーションソフトは、構造解析の場合、ある力学的な問題を数学的に表現した理論をコンピュータのプログラムに実装したものです。そのため、元々の数式が成り立つようにプログラムに入力する条件を揃えてあげないと、シミュレーションできない(数式を解くことができない)のです。
では、シミュレーションを実行するために最低限必要な条件とはなんでしょうか? それはどのような解析を行うのかにもよりますが、ここでは物体の変形や強度を解析する「構造解析(あるいは応力解析)について説明をしていきたいと思います。
●解析に必要な3つの条件
構造解析とは、ものすごくざっくり言うと、一般に何らかの固体でできた部品などに力が加わった時に、その物体内にはどのくらいの大きさの力が発生していて、その影響でどのように変形するのか、あるいは壊れてしまうのか、ということを求めていきます。設計の過程でサクッと解析できるごくシンプルで計算負荷もそれほどかからないものから、挙動そのものをうまくシミュレーションすることが非常に難しく、また計算時間も何日もかかる非常に複雑なものまでさまざまな種類の解析がありますが、すべてに共通する3つの条件があります。以下が揃わなければ解析はできません。
1) 解析形状(解析領域)
2) 材料物性
3) 境界条件(拘束条件・荷重条件)
言われてみれば、当たり前にも思えますが、それでは具体的にはどのようなものを与えればよいのでしょうか?
●解析形状(解析領域)
解析をするためには、当たり前のことですが解析をする対象が必要です。構造解析の場合には、一般にこれは個別の部品であったり、その部品の組み合わせ(アセンブリ)であったりしますが、いずれにしても何か固体でできた物体です。
現在はこれらの形状は3D CADで作成することも多いため、3D CADで作成したジオメトリやアセンブリそのものと言ってもよいでしょう。ただし、シミュレーションソフトの観点から見た時、3D CADで作成したジオメトリはまだ完全ではありません。解析をするためにはこれらのジオメトリを元にして解析用の「メッシュ」を作成する必要があります。「メッシュ」とは解析をするための「要素」の集合体です。要素とは本来は連続体である物体を有限個の非常に小さな六面体や四面体などに離散化したものですが、これら1つひとつの六面体などを要素と言います。
非常に複雑な形であったとしても、小さな六面体の集合体と考え、物体の挙動もこれら1つひとつの要素の挙動の合計として考えれば自由に表すことができるのです。なので、3D CADによる形状を元にしてできた解析メッシュが何はともあれ、必要なものになります。
図1:元のジオメトリ。(クリックで拡大) |
 |

図2:解析メッシュ。(クリックで拡大) |
●材料物性
形ができたら次に考えたいのは、その物体は硬いのか柔らかいのか、などのその形が持つ性質です。最近では、過去に金属で作られていた部品も樹脂に置き換えられたりしているケースも増えてきています。しかし、形状が同じであったとしても、その部品がスチールでできているのか、ABS樹脂でできているのかで、その変形状態や壊れる荷重はまったく違うものになります。ようするにそれらの挙動をきちんと表現し、壊れるのか壊れないのかという指標を与えるための情報が、シミュレーションソフトで使用する材料の物性になります。
これも具体的には解析の種類によりますが、構造解析で言えば、以下のようなものになります。
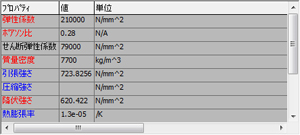
図3:設計者CAEソフトのデータベースの材料物性の例。(クリックで拡大) |
 |
|
・ヤング率(縦弾性係数)
構造解析に用いる材料物性にはさまざまなものがありますが、その中でも絶対に必要なものがこのヤング率です。逆に言えば、この数値さえあれば、他の物性値は必要ないと言っても過言ではありません。金属をはじめとする多くの材料は、荷重をかけると変形し、荷重を除くと元の無変形の形に戻ります。この関係の記述に必要なものがヤング率です。ヤング率は正確には、荷重をかけた時に物体内部に発生する内力(応力)と、その際に発生する変形の度合い(ひずみ)の関係を示しています。この値が大きいほど変形しにくい(剛性が高い)ものということになります。この値は、材料固有のものです。
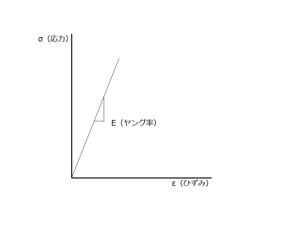
図4:応力・ひずみとヤング率。(クリックで拡大) |
 |
|
・ポアソン比
物体はある方向に引っ張って伸ばすと、それとは直交する方向に縮みます。その比率を示したものがポアソン比です。この値も材料固有です。ポアソン比はなくても計算は成り立ちますが、変形の結果などは不正確になります。
・質量密度
通常はヤング率とポアソン比のみで構造計算は可能ですが、自重による変形や衝撃解析など時間が関係する動解析については、物体固有の質量密度が必要です。この質量密度に体積をかけるとその物体の重量が分かります。
他にもさまざまな物性がありますが、材料物性は上記でごく基本的な解析を行うことが可能です。
●境界条件
・拘束条件
物体の形が定義され、その物体の性質が分かれば、解析の実行まであと一息です。形と物性が決まっただけでは、例えていえば、その物体が宇宙空間に浮いているような状況です。宇宙空間で、どこにも固定されていない物体に力を加えたら、どこまでも飛んでいってしまいますが、そんな状態です。
構造解析では、どこかが固定されていて、力を加えたらどこかに変形することを想定していますが、どこも固定されていないと変形せずに剛体運動を起こしてしまいます。そのため、解析対象となる物体を動かないように固定する必要があります。この固定するための条件のことを「拘束条件」と言います。拘束条件は、3次元での解析の際には、XYZの各並進成分とそれぞれの軸回りの回転成分の合計6つの自由度に対して剛体運動を起こさないように物体をとめる必要があります。
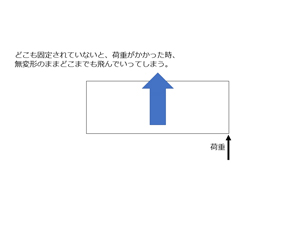
図5:どこも固定されていない状態。(クリックで拡大) |
 |
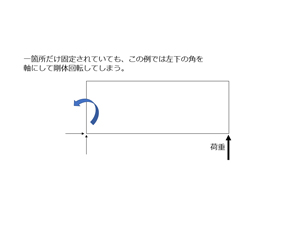
図6:拘束条件が不十分で剛体回転が起きてしまう場合。(クリックで拡大) |
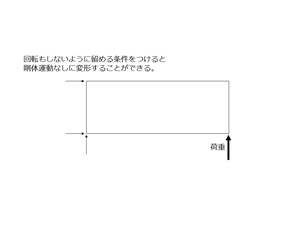
図7:完全に拘束されている場合。(クリックで拡大) |
 |
|
この境界条件のことを、一般に拘束条件と称します。
・荷重条件
必要な拘束条件が定義できても、肝心の外力がかからなければ物体は変形しません。この外力のことを荷重条件と言います。荷重条件には、何キロの力をかける(実際には荷重の単位はニュートンですが)のか、どのくらいのトルクをかけるのかといった荷重値で定義する場合と、力ではなく何ミリここを動かすといった強制変位などがあります。
解析の種類によって、これらの条件はさらに細かく定義されていく場合がありますが、どの解析においても、解析形状、材料物性、境界条件の3つが揃えば解析は可能ですので、あとは現実のモデルをどのようにすれば、解析にモデルにすることができるのかを考えながら、あてはめていくだけです。
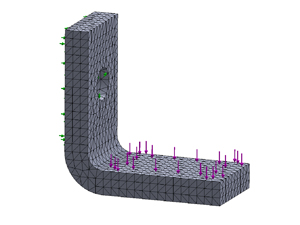
図8:メッシュをはったモデルに拘束条件と荷重条件をかけた例。(クリックで拡大) |
 |
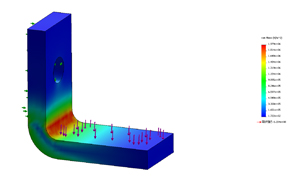
図9:解析に必要な条件を定義して実際に解析を行った例。(クリックで拡大) |
そう考えると、少しだけ解析が身近なものになりませんか?
次回は、解析結果のどこを見ればよいのかを考えていきたいと思います。、
次回は12月中旬掲載予定です。
(2019年11月14日更新)
|



